how to find focus of parabola

Conics: Parabolas:
Finding the Equation from Information (page 3 of 4)

Sections: Introduction, Finding information from the equation, Finding the equation from information, Word problems & Calculators

You will also need to work the other way, going from the properties of the parabola to its equation.

Write an equation for the parabola with focus at (0, �2) and directrix x = 2 .

The vertex is always halfway between the focus and the directrix, and the parabola always curves away from the directrix, so I'll do a quick graph showing the focus, the directrix, and a rough idea of where the parabola will go:

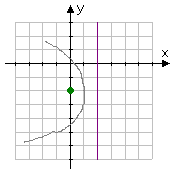
focus in green, directrix in purple, with a rough sketch of where the graph will go

So the vertex, exactly between the focus and directrix, must be at (h, k) = (1,
�2) . The absolute value of p is the distance between the vertex and the focus and the distance between the vertex and the directrix. (The sign on p tells me which way the parabola faces.) Since the focus and directrix are two units apart, then this distance has to be one unit, so | p | = 1 .

Since the focus is to the left of the vertex and directrix, then the parabola faces left (as I'd shown in my picture) and I get a negative value for p : p = �1 . Since this is a "sideway" parabola, then the y part gets squared, rather than the x part. So the conics form of the equation must be:

( y � (�2))² = 4(�1)(x � 1) , or ( y + 2) ² = �4( x � 1)

Write an equation of the parabola with vertex (3, 1) and focus (3, 5) .

Since the x -coordinates of the vertex and focus are the same, they are one of top of the other, so this is a regular vertical parabola, where the x part is squared. Since the vertex is below the focus, this is a right-side up parabola and p is positive. Since the vertex and focus are 5 � 1 = 4 units apart, then p = 4 . Copyright � Elizabeth Stapel 2010-2011 All Rights Reserved

And that's all I need for my equation, since they already gave me the vertex.

(x � h)² = 4p(y � k)
(x � 3)² = 4(4)(y � 1)
( x � 3) ² = 16( y � 1)

Write an equation for the parabola with vertex (5, �2) and directrix y = �5 .

The directrix is an horizontal line; since this line is perpendicular to the axis of symmetry, then this must be a regular parabola, where the x part is squared.

The distance between the vertex and the directrix is |�5 � (�2)| = |�5 + 2| = 3 . Since the directrix is below the vertex, then this is a right-side up parabola, so p is positive: p = 3 . And that's all I need to find my equation:

(x � h)² = 4p(y � k)
(x � 5)² = 4(3)(y � (�2))
( x � 5) ² = 12( y + 2)

<< Previous Top | 1 | 2 | 3 | 4| Return to Index Next >>

Cite this article as:

Stapel, Elizabeth. "Conics: Parabolas: Finding the Equation From Information." Purplemath.
Available from https://www.purplemath.com/modules/parabola3.htm .
Accessed